-
Définition
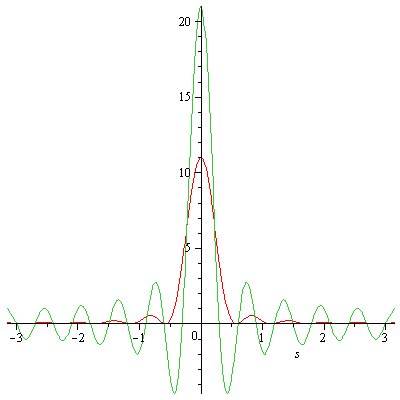
Noyau de Fejér : $${{\mathscr K_N(\theta)}}={{\frac1N\sum^{N-1}_{n=0}\mathscr D_n(\theta)}}={{\underbrace{\sum^{N-1}_{\lvert n\rvert\lt N}\frac{N-\lvert n\rvert}Ne^{in\theta} }_{\text{somme de Cesàro} } }}$$
(
Noyau de Dirichlet)
Propriétés
Convolution
$${{\mathscr K_N*f(\theta)}}={{\sigma_N f(\theta)=\underbrace{\sum_{\lvert n\rvert\leqslant N}\frac{N-\lvert n\rvert}NF_ne^{in\theta} }_{\text{somme de Cesàro} } }}$$
(
Convolution,
Sommation de Cesàro)
Positivité
$$\mathscr K_N(\theta)\geqslant{{0}}\quad\text{ pour }\quad\theta\in\Bbb T$$
Intégrale
$$\int_\Bbb T\lvert \mathscr K_N\rvert={{2\pi}}$$
Limite
$$\lim_{N\to+\infty}\mathscr K_N(\theta)={{0}}\qquad\text{ si }\qquad {{\theta\ne0}}$$
Cette limite est uniforme
-
Rétroliens : 